Riapriamo il vastissimo libro della fisica della palla durante una partita di tennis. Nella prima parte di questa analisi ci siamo soffermati sostanzialmente sulla fisica del rimbalzo, che per forze e fattori in gioco è anche l’unica riproducibile in laboratorio e la più semplice da modellizzare. Ne conviene che è anche più agevole trarre delle conclusioni: ci siamo infatti accorti che l’utilizzo smodato del topspin diminuisce la differenza tra superfici, pure in presenza di caratteristiche fisiche (attrito, coefficiente di restituzione) apprezzabilmente differenti.
Come però hanno giustamente sottolineato molti lettori, non c’è solo il rimbalzo. Il comportamento globale della palla è influenzata da tantissimi altri fattori. I tornei utilizzano palle diverse. Una stessa superficie di gioco può essere ‘montata’ su strati profondi differenti che modificano il comportamento della palla. Ma soprattutto, ed è il tema che affronteremo in questo articolo, possono cambiare le condizioni atmosferiche: temperatura, pressione, umidità, altitudine.
Partiremo da una breve premessa sulle forze che regolano la traiettoria della palla per poi approfondire l’impatto delle condizioni atmosferiche. Nel terzo e ultimo articolo, che chiuderà questa mini-serie sulla fisica applicata al tennis, faremo qualche considerazione sulla terra battuta, la superficie sulla quale il circuito è attualmente impegnato.
Buona parte delle nostre considerazioni partono da questi paper (1 e 2) di Rod Cross e dall’articolo di approfondimento dell’utente Twitter @fogmount. Il resto è farina del nostro sacco, speriamo non troppo disprezzabile.
PRIMO BLOCCO: LE TRAIETTORIE DELLA PALLA
Nonostante possa sembrare banale tenere la palla in campo, in realtà dal punto di vista fisico esiste un range molto ristretto di angoli e di velocità a cui è necessario colpire la palla per far sì che superi la rete e atterri prima della riga di fondo. Ricordiamo che il campo è lungo poco meno di 24 metri (23.77), la distanza tra rete e riga di fondo è dunque di 11.887 metri e la rete è alta 0,914 m al centro e 1,07 m ai lati. Il nostro cervelletto e le nostre capacità coordinative visuo-motorie non sanno risolvere equazioni, ma svolgono in modo empirico i calcoli necessari a colpire la palla con successo.
La facciamo breve con un esempio: per una palla colpita da un metro d’altezza, dalla riga di fondo e a circa 108 km/h, esiste un range di 4,1° di inclinazione del colpo (rispetto al piano orizzontale) per tenerla in campo se colpiamo senza rotazione, e di 6,4° se utilizziamo un po’ di topspin (circa 1200 rpm).
Dal confronto tra i range si evince una prima verità intuibile anche senza consultare i manuali di fisica: un colpo in topspin è più sicuro, ovvero ha un margine d’errore più ampio. Possiamo aggiungere un altro mattoncini e dirvi che, ad esempio, servire dai lati del campo sembra soltanto più difficile; è vero che la rete da superare è leggermente più alta, ma è anche vero che aumenta la distanza dal quadrato dal servizio e con essa gli angoli disponibili.
Chiaramente la faccenda è più complessa di così. I dati del primo esempio provengono da un modello ideale in cui non si prende in considerazione l’attrito dell’aria. Che invece esiste, ha una grande importanza e soprattutto complica terribilmente il tutto.
Un po’ di fisica (non sbadigliate)
Per calcolare precisamente la traiettoria di un corpo in volo bisogna prendere in esame la componente orizzontale e la componente verticale dello spostamento (espresso sotto forma di accelerazione, orizzontale e verticale). Concettualmente il discorso è simile alla fisica del rimbalzo, ambito in cui avevamo però parlato solo di velocità, orizzontale e verticale.
In entrambe le equazioni, quella dell’accelerazione orizzontale (eq.1) e quella dell’accelerazione verticale (eq.2) le variabili in gioco sono il raggio della palla (R), la sua velocità (v), la densità dell’aria (ρ) e il coefficiente di resistenza dell’aria (CD, o drag coefficient). Le variabili si combinano nelle equazioni (eq. 3 e 4) che servono a calcolare le due forze FD e FL, meglio note come ‘Drag force’ e ‘Lift force’: sono le due componenti di forza che esprimono l’attrito dell’aria parallelamente al moto del corpo (FD) e perpendicolarmente (FL).
Lo ammettiamo, è abbastanza complicato, ma attraverso questo diagramma ci si può fare un’idea visiva delle forze in gioco. Aggiungiamo che nell’equazione dell’accelerazione verticale entra in gioco anche l’attrazione gravitazionale (mg), l’unico valore che dipende dalla massa della palla.
eq. 1 – ax = −FD cosθ − FL sinθ
eq. 2 – ay = FL cosθ − FD sinθ − mg
eq. 3 – FD = 1/2 CDρπR2v2
eq. 4 – FL = 1/2 CLρπR2v2
Volendola semplificare al massimo, una palla colpita da una racchetta è un corpo che cerca di fendere l’aria – la quale oppone una certa resistenza, poiché è a tutti gli effetti un fluido con un suo peso (una stanza di medie dimensioni piena d’aria arriverebbe a pesare anche un centinaio di chili). Se alle solite velocità di un match di tennis questa resistenza (espressa del coefficiente CD di cui vi abbiamo già parlato) è grossomodo indipendente dalle piccole differenze di velocità tra un colpo e l’altro, dunque più o meno costante, le cose cambiano (di nuovo!) se prendiamo in esame le rotazioni e dunque il coefficiente CL (lift coefficient). Cambiano perché entra in gioco l’effetto Magnus.
Quando una palla ‘fora’ l’aria, quest’ultima si precipita in qualche modo a riempire lo spazio lasciato vuoto dalla palla. Se la palla è in rotazione, però, il flusso dell’aria si comporta in modo diverso. Nel caso di un colpo in topspin, l’aria viene deviata maggiormente verso l’alto e questo crea una depressione che spinge la palla verso il basso, dunque ad atterrare prima; nel caso di un backspin avviene invece l’opposto, l’aria è spinta verso il basso e dunque la palla riceve una spinta verso l’alto, che la porta a ‘galleggiare’ di più nell’aria e atterrare più tardi. Questo è uno dei motivi per cui le difese disperate in back sono più efficaci (è più facile che superino la rete rispetto al top) ma tenere il controllo di un back offensivo è più difficile, perché la palla tende a scappare in lunghezza.
Inoltre la superficie delle palle da tennis, alquanto irregolare, contribuisce ad aumentare l’effetto Magnus rispetto a una palla liscia come può essere quella da baseball. La classica peluria contribuisce anche a normalizzare il drag coefficient, che abbiamo già assunto essere più o meno costante alle velocità comuni di un match di tennis; come risultato finale, per un tennista è un po’ più semplice intuire la traiettoria di un colpo rispetto, ad esempio, alle previsioni che è costretto a fare un catcher. Per capirci, in questo senso Jaden Agassi dovrà faticare più di papà Andre: per sua fortuna è un lanciatore, e sempre per sua fortuna dovrebbe aver ereditato una coordinazione mano-occhio di primissima classe.
SECONDO BLOCCO: LE CONDIZIONI ATMOSFERICHE
Esaurite le premesse fisiche, e sperando di essere stati chiari e di non avervi annoiato troppo, andiamo in campo. E affrontiamo la questione relativa alle condizioni atmosferiche partendo dalle tre caratteristiche principali dell’aria che circonda i tennisti: temperatura, umidità e pressione, che contribuiscono a far variare ρ (densità dell’aria).
Umidità, temperatura e pressione
È opinione piuttosto diffusa che l’aria umida sia più pesante, tanto da respirare quanto da perforare con un missile di dritto. Nulla di più sbagliato: l’aria umida, che contiene più molecole di vapore acqueo (H20, peso molecolare 18), è più leggera dell’aria secca che consiste quasi interamente in molecole di azoto (N2, pm 28) e ossigeno (02, pm 32). Semmai, dunque, per la palla è più facile fendere l’aria umida.
Oltre a essere opposto rispetto a quello che si immagina, l’effetto dell’umidità sulla velocità della palla è anche trascurabile. Considerando le condizioni di temperatura a cui abitualmente si gioca a tennis, un aumento di umidità dallo 0 al 100% in una giornata in cui ci sono 21°C produrrebbe una diminuzione della densità dell’aria di appena l’1% e aumenterebbe la velocità di un drittone da fondo di meno di mezzo chilometro orario. L’effetto diventerebbe un po’ più apprezzabile partendo da temperature più alte, ma sono condizioni in cui di solito non si gioca a tennis, e se per caso è in corso un torneo di solito gli incontri vengono fermati per effetto delle heat rules.

A voler essere davvero pignoli, l’umidità ha anche un lievissimo effetto sul diametro della palla (lo riduce, ma in modo appena misurabile e quindi ininfluente ai fini dei nostri calcoli) e sul suo peso, aumentandolo, poiché la palla umida assorbe qualche molecola d’acqua. Nulla che possa modificare in modo sostanziale le equazioni che vi abbiamo illustrato più in alto.
La temperatura incide invece molto di più sulla densità dell’aria. Passando da 10 a 38°C, la densità dell’aria diminuisce di circa il 10% e i colpi possono guadagnare anche 3-5 km/h di velocità. Anche la pressione atmosferica – abbassandosi – può far decrescere parecchio la densità dell’aria, ma sul pianeta Terra i valori di pressione sono così uniformi che il tennis non raccoglie i frutti di questo principio (quando si passerà a giocare su Marte, magari, ne riparleremo).
Conclusioni (e condizioni ‘pesanti’)
Riassumendo: quando fa caldo la palla viaggia più rapidamente e la differenza si sente, quando è umido la palla diventa (poco) più veloce ma la differenza è praticamente impercettibile.
Per contrasto, in condizioni di temperatura rigide i giocatori sperimentano una certa difficoltà nel generare velocità con la palla che è perfettamente in linea con quanto illustrato. Una difficoltà che si esacerba ulteriormente quando fa freddo e magari pioviggina anche un po’, come in occasione del Roland Garros 2020 che si è disputato in pieno autunno e in condizioni molto dure.
Se dal cielo vien giù qualche goccia, oltre al piccolo contributo di cui abbiamo già parlato se l’aria è anche umida, la palla può effettivamente appesantirsi. Applicando però l’aumento di massa compatibile con una leggera pioggerellina alle equazioni di cui sopra, non si ottiene un effetto tanto importante da spiegare la ‘selezione’ che è in grado di fare una giornata di tennis che si disputa in condizioni pesanti, simile a un tappone di montagna. Le avete presente, quelle giornate in cui restano in piedi solo i più strutturati fisicamente e quelli che hanno muscoli e chili per far viaggiare la palla?
L’ipotesi di @fogmount, che ci sentiamo di condividere, è che le palle ‘pesanti’ complichino i piani dei giocatori più nel senso del logoramento. Se la percentuale di forza in più che è necessario impartire alla palla per generare la stessa velocità è minima sul singolo colpo, non lo è più nell’arco di un set o di una intera partita. Banalmente, i giocatori meno preparati atleticamente accusano la fatica prima di chi ha chili e struttura per tirare pallate per tre ore, anche quando le palle sono dure come pietre e grandi come cocomeri.
L’altitudine
Prima di darvi appuntamento alla terza e ultima puntata, però, vorremmo dedicare due righe alla variabile che più di tutte sembra incidere sulle condizioni di gioco: l’altitudine. Dai quasi 600 metri sul livello del mare di Madrid agli oltre 2500 di Bogotá, c’è una manciata di altri tornei che si disputa in condizioni in cui l’aria è un pizzico più rarefatta e dunque meno densa. Come avete già appreso, ci aspettiamo che la palla viaggi più rapidamente: infatti accade, e l’aumento di velocità è percentualmente superiore a quello imputabile alla temperatura.
Vi proponiamo un’altra simulazione computerizzata al fine di comparare l’aumento di velocità per un colpo piatto e per un colpo in topspin (4000 rpm).
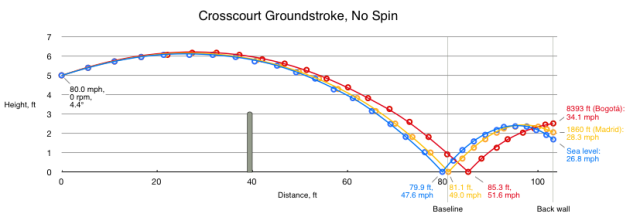
Partiamo da un drittone piatto tirato a circa 130 km/h sul livello del mare, a Madrid e a Bogotá. Il computer dice che in Colombia la sberla ha una velocità superiore di 6,5 km/h al momento del rimbalzo (rispetto al livello del mare) e di oltre 11 quando raggiunge lo sfortunato avversario; la differenza di altezza del rimbalzo è minima, mentre la rarefazione dell’aria incide anche sulla lunghezza del colpo che è più difficile da tenere in campo (perché l’aria esercita meno attrito).
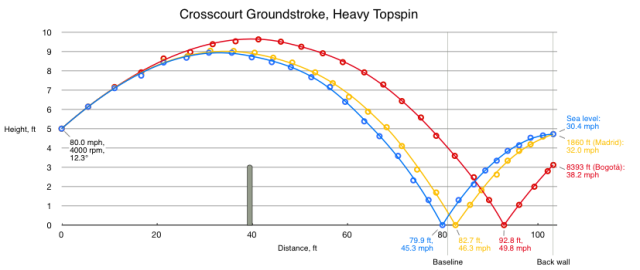
Prima di esaminare cosa succede al drittone carico giocato sempre a 130 km/h, occorre sottolineare che per generare la stessa velocità e impartire allo stesso tempo tanta rotazione serve molta potenza in più, motivo per cui certe cose le vediamo fare soltanto a Nadal e pochi altri.
Ebbene, in questo caso il dritto colombiano arriva al ribattitore addirittura con una velocità superiore di quasi 13 km/h; una differenza molto importante, compensata però dal fatto che quel drittone, molto poco frenato dalla rarefatta aria sudamericana, finirebbe lungo di tre metri buoni. Insomma, è più facile tirare topponi veloci a Bogotá ma è più difficile tenerli in campo, quindi tocca tarare il braccio. Resta un dato incontrovertibile: se volete finalmente prendere a pallate quel vostro amico che vi porta all’esasperazione – e al gratuito sistematico – quando vi sfidate in primavera sul lungomare di Cattolica, più che aspettare il solleone estivo dovreste portarlo… a Bogotá. Magari voi andateci un mese prima: prima di tutto per acclimatarvi, perché respirare in quota è più dura, e poi per capire come domare i nuovi cavalli del vostro dritto!
Alla prossima puntata: come promesso, parleremo (quasi) solo di terra.










